Notes on combining sequential and simultaneous moves

As part of a series of discussions on Games of Strategy, I've written here about games with sequential moves - those in which players "take turns" and each decision is made with full knowledge of the opponent's last decision - as well as games with simultaneous moves - those in which players make decisions not knowing which option an opponent has selected. Continuing our exploration of game theory, Dr. Wictz and I further discussed games that combine sequential and simultaneous moves.

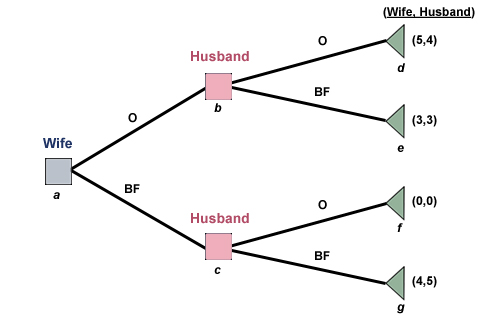
Game tree for "Battle of the Sexes"
Source: "Managerial Economics Online,"
kwanghui.com/mecon

A simultaneous move pure strategy game can be converted into a sequential move game, which can change the outcome depending on the payoff matrix. When "The Battle of the Sexes" is a simultaneous coordination game (like "Will Harry Meet Sally?"), there are two equilibria, and the outcome is indeterminate. When it is sequential, the player moving first will select the option they prefer, and the player moving second will follow suit because it becomes the only beneficial option. The result is a first-player advantage, meaning that the player moving first maximizes their payoff.

Suppose the tennis match we looked at in our examination of mixed-strategy games were converted into a sequential move game, perhaps because the defender can react quickly enough to defend either shot regardless of what the shooter decides to do. Then, by rollback analysis, the shooter will be motivated always to choose the shot that the defender is less effective at defending, and then the defender will defend it. The result is a second-player advantage; the first player can never maximize their payoff because the second player can always respond. If, on the other hand, a slower defender has a "tell" and commits to a defense before the shooter decides on their shot, then the shooter can always attack the weak side of the defense and maximize their payoff - again, a second-move advantage.

Recalling that we can model sequential games as a decision-tree network, we then can represent each node of the sequential game as a simultaneous game decision matrix whose outcome determines the next branch of the sequential game. We discussed The Resistance, a hidden-identity game that consists of a sequence of simultaneous-decision games. The decision tree extends over five rounds in which each team seeks to win three rounds. Each round can itself be thought of as a sequential decision tree of simultaneous decisions - first voting whether to accept a mission team, and second among those on the team, deciding whether to support or sabotage the mission.

A sequential game can have an equilibrium path that can be determined by roll-back analysis - pruning non-optimal branches of the tree from the end backward to the beginning. I described this processes in my discussion of bidding and game theory. But a sequential game can also proceed along an "off-equilibrium path" if players make non-optimal decisions - more common in complex games where the decision tree or simultaneous decision matrix defies complete analysis.

A subgame is defined as part of a multi-move game that begins at a particular decision-tree node of the original game. A "subgame-perfect equilibrium (SPE)" is a set of strategies - one for each player - that defines the optimal decision at each node in the decision tree, whether or not that node is on the equilibrium decision tree path. No matter where the game may start, for every subgame, the SPE defines the optimal strategies for both players.

Considering our Resistance example, information is incomplete, so players generally will signal intent in attempts to steer one another along a decision path to a subgame that is closer to their own best result. The success of those attempts depends on the credibility of the signal, and therein lies the heart of such social interactive games.